Certainement la plus simple à appliquer, celle-ci est simplement une application de la couleur ambiante sur l'objet à éclairer.

couleurAmbiante = lumiere.ambiant;

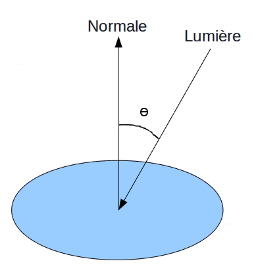
La lumière diffuse est une application de la formule de la réflexion de Lambert :

• intensité = couleur_de_la_lumière_diffuse * cos(angle_entre_le_rayon_de_la_lumière_et_la_normale_de_l'objet)

Comme vous pouvez le constater, la couleur que l'on applique sur le pixel n'est qu'une fraction de la lumière de la lampe. La fraction dépend de l'angle entre le rayon lancé par la lampe sur l'objet et de l'orientation de l'objet (sa normale).

Le rayon de la lumière n'est autre que le vecteur entre la lumière et le point d'impact de celle-ci. Il est simple de connaître ce vecteur car nous avons la position de la source de lumière mais aussi la position du point de rebond. Ce point est exactement celui dont nous calculons l'intensité de la lumière. L'opération sera donc :

Vec3 rayon = lumiere.position – vertex;

(Note : La position du la lumière doit être normalisée)

Pour connaître le cosinus de l'angle entre deux vecteurs nous allons utiliser le produit scalaire (en anglais : dot product). Le GLSL nous fournit une fonction appelé 'dot' pour appliquer ce calcul. Nous aurons donc dans notre code :

float angleLumiere = dot(normal, rayon);

Finalement, nous pouvons appliquer la formule de la réflexion de Lambert :

Vec3 couleurDiffuse = lumiere.diffuse * angleLumiere;

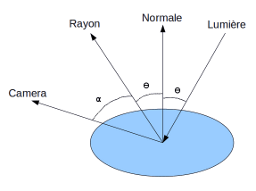
La lumière spéculaire est le reflet de la lampe sur l'objet que nous dessinons. Pour calculer celle-ci nous utilisons le modèle simplifié Blinn-Phong. La formule de ce modèle est la suivante :

• spec = (Normale . (Oeil – rayon_lumière))^shininess * couleur_de_la_lumière_speculaire

Pour connaître la position de l'œil, nous allons utiliser la position du vertex que nous sommes actuellement entrain de calculer pour lui appliquer la matrice inverse de vue. Pour rappel, la matrice de vue, permet de transformer des coordonnées de l'espace monde à l'espace de la caméra. La multiplication avec la matrice inverse fait donc l'opération inverse, ainsi, nous pouvons retrouver la position de la caméra. Le code de cette opération est le suivant :

Vec3 oeil = matrice_inverser_vue * vertex;

Le rayon_lumière, qui représente le vecteur entre la lumière et l'objet se calcule en soustrayant la position de la lumière à celle du vertex :

Vec3 ray = lumiere.position – vertex;

Le reste de la formule ne pose pas de problème. Pour rappel, afin d'effectuer les calculs sur les puissances le GLSL fournit la fonction pow (pour 'power' qui signifie puissance en anglais). La variable appelée 'shininess' correspond à la force du reflet.

vec3 couleurSpeculaire = pow(dot(normale,(oeil-ray)),lumiere.shininess) * lumiere.couleurSpeculaire;

Voici les résultats avec un shininess de 8, 64 et 128 :

Le calcul final de la couleur se résume à la somme des différentes lumières. Toutefois, la lumière spéculaire ne doit pas apparaître si l'angle de la lumière (défini lors du calcul de la lumière diffuse) est inférieur à zéro (il serait dommage de voir le reflet de la lampe alors que celle-ci éclaire l'autre face de l'objet).

gl_FrontColor = couleurAmbiante + couleurDiffuse + couleurSpeculaire;

Maintenant que nous savons comment calculer les différentes lumières, nous allons découvrir comment reproduire les différents types de lampe. Les formules que nous avons apprises juste ci-dessus sont appliquées dans les trois cas, seulement des effets d'atténuation, ou de limite sont ajoutés.

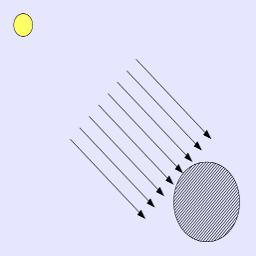
La lampe directionnelle peut être comparée au soleil. Ainsi nous pouvons prétendre que la lumière est à une distance infinie, ce qui nous permet de considérer tout les rayons parallèles et ne subissant aucune atténuation. Pour l'appliquer, nous n'avons besoin que de la direction de ses rayons (ou de la position de la lampe). Cela nous simplifie énormément les calculs.

En fait, comme il s'agit d'une lampe sans atténuation, qui éclaire le monde entier, les calculs de la lumière peuvent être effectués tels qu'ils ont été présentés précédemment.

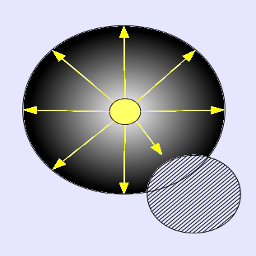
Cette lampe ne se base que sur la distance des objets. Selon cette distance, l'objet sera plus ou moins éclairé. De plus, cette lampe éclaire dans toutes les directions.

Comme vous avez pu le deviner, il nous faut calculer la distance de la lampe à l'objet :

Vec3 vLumObj = lumiere.position – vertex ;
                  float distance = length(vLumObj);

Puis, encore une fois, nous allons calculer l'atténuation selon cette distance :

float attenuation = lumiere.attenuationConstante  +
                  lumiere.attenuationLineaire * d +
                  lumiere.attenuationQuadratique * d * d;

Finalement, nous n'avons plus qu'à appliquer cette atténuation sur la lumière :

couleurAmbiante = couleurAmbiante * attenuation ;
                  couleurDiffuse = couleurDiffuse * attenuation ;
                  couleurSpeculaire = couleurSpeculaire * attenuation;

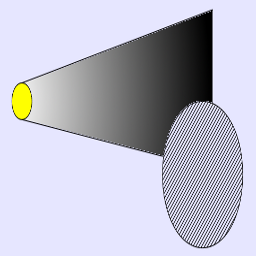
Le spot peut être représenté par un cône ayant la pointe à la source de la lampe. Si l'objet éclairé est au centre du cône, il reçoit la lumière « forte », mais si celui-ci est sur les bords, la couleur de la lumière est atténuée.

Déjà vous pouvez vous douter des besoins d'une telle lampe. Il nous faut :

• la direction de la lumière;
• l'angle d'ouverture du cône ;
• atténuation constante ;
• atténuation linéaire ;
• atténuation quadratique ;
• une limite d'éclairage ;
• un coefficient d'exposition.

Commençons par récupérer la distance entre notre lampe et notre objet. Lors du calcul du rayon de la lumière, nous avons vu comment récupérer le vecteur entre la lumière et l'objet. Pour calculer la distance à partir d'un vecteur, le GLSL nous fournit une fonction toute prête : length() (qui signifie 'distance' en anglais).

Vec3 vLumObj = lumiere.position – vertex ;
float distance = length(vLumObj);

Maintenant, nous allons calculer l'atténuation selon la distance de l'objet. Pour cela, nous allons reprendre la formule utilisée par OpenGL dans son pipeline fixe.

float attenuation = lumiere.attenuationConstante  +
lumiere.attenuationLineaire * d +
lumiere.attenuationQuadratique * d * d;

Ensuite nous devons savoir si l'objet est dans le cône de lumière de la lampe. Pour cela nous allons calculer l'angle entre le vecteur de la position de la lampe à l'objet et le vecteur entre l'objet et la direction de la lampe. Encore une fois, nous utilisons le produit scalaire :

float angle = dot(-vLumObj, normalize(lumiere.direction));

Nous allons calculer une deuxième atténuation qui, cette fois, dépend de l'angle entre le spot et l'objet.

float spotAttenuation = 0.0f
if ( angle >= lumiere.limite )
{
    spotAttenuation = pow(angle,lumiere.exposition);
}

Nous appliquons cette atténuation sur la première que nous avions trouvée :

attenuation *= spotAttenuation;

Pour finir, nous appliquons l'atténuation dans notre calcul de la lumière :

couleurAmbiante = couleurAmbiante * attenuation ;
couleurDiffuse = couleurDiffuse * attenuation ;
couleurSpeculaire = couleurSpeculaire * attenuation;

Il nous reste une toute petite partie (optionnelle) lors du calcul de l'effet de lumière sur notre objet. Actuellement, dans nos calculs de lumière nous n'avons pas pris en compte la couleur de nos objets. Plus précisément, nous parlons de matériaux, car les objets peuvent réfléchir de différente manière la lumière.

Pour décrire un matériau il faut définir :

• la couleur;
• la couleur diffuse (celle qui est renvoyé à l'œil) ;
• la couleur spéculaire (une altération du reflet de la lumière, par le matériau).

Pour appliquer un matériau, il faut juste suivre la formule suivante :

(Je pars du principe, que les différentes couleurs contiennent les valeurs précédentes de nos calculs de lumière). La structure pour les matériaux peut être la suivante :

struct Materiaux
{
    vec4 ambiante;
    vec4 diffuse;
    vec4 speculaire;
}

couleurAmbiante = couleurAmbiante * mat.ambiante;
couleurDiffuse = couleurDiffuse * mat.diffuse;
couleurSpeculaire = couleurSpeculaire * mat.speculaire;

Notez qu'encore une fois, il faut que la lumière spéculaire ne soit visible que si l'angle est supérieur à 0.

Nous avons vu les différentes lumières et les différents types d'éclairages qui étaient présent dans le pipeline fixe d'OpenGL. Vous pouvez implémentez vos propres effets afin d'avoir le résultat qui vous convient le mieux. Le site wikipedia regorge d'informations sur ce sujet en perpétuel évolution.

Les algorithmes décris dans cette section peuvent être appliqué dans le vertex shader ou dans le pixel shader. Sachant que le pixel shader est exécuté pour tous les pixels dessinés, l'exécution sera plus lente, par contre, ce sera plus beau.

L'ancien pipeline était limité à 8 lampes. Maintenant vous pouvez faire plus, mais cela va ralentir l'exécution. Il existe une méthode appelé « rendu différé » (Deferred Shading) permettant de mettre des centaines de lampes dans une scène.

Dans le pipeline fixe d'OpenGL, nous avions la possibilité de choisir la façon dont la couleur de la texture allait être appliquée sur notre objet. Je vais retranscrire rapidement les différentes formules.

GL_REPLACE :

Remplace la couleur actuelle par la couleur de la texture. C'est exactement le calcul que j'ai fait dans l'exemple précédent.

Couleur = texture2D(tex0, gl_TexCoord[0].xy) ;

GL_MODULATE :

Multiplie la couleur venant du vertex shader avec cette de la texture. Cela peut être utile si le calcul de la lumière est effectué dans le vertex shader, et que cette lumière doit avoir un effet sur l'application de la texture.

couleur *= texture2D(tex0, gl_TexCoord[0].xy) ;

GL_DECAL :

Utile dans le cas où vous voulez afficher la texture d'un logo sur une surface. La valeur alpha de la texture est utilisée pour faire une interpolation entre la couleur venant du vertex shader (gl_Color), et la couleur de la texture. Finalement, la valeur alpha du vertex shader est utilisée.

Vec4 couleurText = texture2D(tex0, gl_TexCoord[0].xy) ;
vec3 coul = mix(color.rgb, couleurText.rgb, couleurText.a) ;
couleur = vec4(coul, color.a);

GL_BLEND :

Ce mode prend en compte la couleur de la texture de l'environnement, en faisant une interpolation entre la couleur venant du vertex shader et celle-ci. Le facteur pour l'interpolation est la texture. Finalement la couleur alpha est déterminée par la multiplication de l'alpha entrant et celui de la texture.

Vec4 couleurText = texture2D(tex0, gl_TexCoord[0].xy) ;
vec3 coul = mix(color.rgb, gl_TextureEnvColor[0].rgb, couleurText.rgb) ;
couleur = vec4(coul, color.a * couleurText.a);

GL_ADD :

Ajoute simplement les couleurs. La composante alpha est multiplié pour calculer la composante alpha résultante. Finalement nous remettons les valeurs dans l'intervalle [0, 1] car le calcul peut engendrer des résultats trop grand.

Vec4 couleurText = texture2D(tex0, gl_TexCoord[0].xy) ;
color.rgb *= couleurText.rgb;
color.a *= couleurText.a ;
couleur = clamp(color,0.0, 1.0);

Depuis OpenGL 1.3, il y a de nouveau mode d'application de texture. Ils ne sont pas décrits ici, car cela sort du cadre de ce tutoriel. De plus, il est facile de deviner leur implémentation selon leurs descriptions.

Dans OpenGL, nous pouvions demander au pipeline de générér automatiquement les coordonnées de texture. Si vous voulez toujours utiliser cette méthode (qui présente quelques défauts), voici comment faire.

Pour rappel, OpenGL définit 5 types de génération :

• GL_OBJECT_LINEAR : utile lorsque la texture est fixé à l'objet (par exemple : un terrain) ;
• GL_EYE_LINEAR : utile pour produire des contours dynamiques aux objets ;
• GL_SPHERE_MAP : peut générer des coordonnées pour l'application d'environnement ;
• GL_REFLECTION_MAP : utilise le vecteur de réflexion comme coordonnées de texture ;
• GL_NORMAL_MAP : utilise la normale comme coordonnée.

Le calcul pour une sphère, tel qui est décrit dans la spécification d'OpenGL est le suivant :

vec2 sphereMap(in vec3 cameraPosition, in vec3 normal)
{
     float m ;
     vec3 r, u ;
     u = normalize(cameraPosition) ;
     r =reflect(u, normal) ;
     m = 2.0 * sqrt(r.x * r.x + r.y * r.y + (r.z + 1.0) * (r.z + 1.0)) ;
     return vec2(r.x / m + 0.5, r.y / m + 0.5);
}

Le calcul utilisé pour GL_REFLECTION_MAP est :

vec3 reflectionMap(in vec3 cameraPosition, in vec3 normal)
{
     vec3 u = normalize(cameraPosition) ;
     return (reflect(u,normal));
}

Finalement, selon le choix que vous faites pour votre génération, le code généraliste pour avoir les coordonnées de texture est le suivant :

vec2 sphereMapCoord ;
vec3 reflectionCoord;
 
If ( isTexSphere )
{
    sphereMapCoord = sphereMap(cameraPosition,normal);
}
 
if ( isTexReflection )
{
    reflectionCoord = reflectionMap(cameraPostion,normal);
}
 
// Pour toutes les textures activées
for ( int i = 0 ; i < nombreTexture ; i++ )
{
    if ( isTexObject )
    {
        gl_TexCoord[i].s = dot(gl_Vertex, gl_ObjectPlaneS[i]) ;
        gl_TexCoord[i].t = dot(gl_Vertex, gl_ObjectPlaneT[i]) ;
        gl_TexCoord[i].p = dot(gl_Vertex, gl_ObjectPlaneR[i]) ;
        gl_TexCoord[i].q = dot(gl_Vertex, gl_ObjectPlaneQ[i]);
    }
 
    if ( isTexEye )
    {
        gl_TexCoord[i].s = dot(gl_Vertex, gl_EyePlaneS[i]) ;
        gl_TexCoord[i].t = dot(gl_Vertex, gl_EyePlaneT[i]) ;
        gl_TexCoord[i].p = dot(gl_Vertex, gl_EyePlaneR[i]) ;
        gl_TexCoord[i].q = dot(gl_Vertex, gl_EyePlaneQ[i]);
    }
 
    if ( isTexSphere )
    {
        gl_TexCoord[i] = vec4(sphereMapCoord, 0.0, 1.0);
    }
 
    if ( isTexReflection )
    {
        gl_TexCoord[i] = vec4(reflectionCoord, 1.0);
    }
 
    if ( isTexNormal )
    {
        gl_TexCoord[i] = vec4(normal, 1.0);
    }
}